Rabin加密体制原理概述
概述
Rabin 密码系统是第一个非对称密码系统,由Michael Oser Rabin于1979年在论文*Digitalized Signatures and Public-Key Functions as Intractable as Factorization*中发表。可以证明从密文中恢复明文与分解一样困难,它的安全性来源于大整数的因子分解。优点:
Rabin 函数的每个输出都可以由四个可能的输入中的任何一个生成
如果每个输出都是密文,则解密时需要额外的复杂性来识别四个可能的输入中的哪一个是真正的明文
密钥生成算法
Rabin密码系统的密钥生成如下:
1. 选择两个不同的大素数 𝑝 和 𝑞 ,并且满足 𝑝≡3 mod 4和 𝑞≡3 mod 4
2. 计算 𝑛 = 𝑝×𝑞.
将 𝑝 和 𝑞 作为私钥,n 作为公钥。
一个消息 M 首先转换为数字 m (m < n, 可逆映射),然后计算. 密文为 c .
消息 m 可以从密文中 c 通过取其平方根模 n 如下。
$$
\begin{equation}
\begin{aligned}
&m_{p 1}=c^{\frac{1}{4}(p+1)} \bmod p, \ m_{p 2}=\left(p-m_{p 1}\right) \bmod p \\
&m_{q 1}=c^{\frac{1}{4}(q+1)} \bmod q, \ m_{q 2}=\left(q-m_{q 1}\right) \bmod q
\end{aligned}
\end{equation}
$$
求出四个 m 后两两使用中国剩余定理求解,则得到消息 m 的四个可行解。
这四个值之一是原始明文 m,在没有额外信息的情况下无法确定这四个中的哪一个是正确的。如果明文意在代表一条短信,猜测不难;然而,如果明文旨在表示一个数值,这个问题就成为一个必须通过某种消歧方案来解决的问题。可以选择具有特殊结构的明文,或者添加padding(填充)来消除这个问题。这是 Rabin 密码系统的主要缺点。
模 p 平方根证明
因为 p 是形如素数,所以存在奇数 s 使得即
$$
\begin{equation}
p-1=2s
\end{equation}
$$
现在同余式
$$
\begin{equation}
m^2\equiv c\ (mod\ p)
\end{equation}
$$
有解,则根据欧拉判别条件,有
$$
\begin{equation}
c^\frac{p-1}{2}\equiv c^s\equiv1\ (mod\ p)
\end{equation}
$$
两端同时乘以 c 得到
$$
\begin{equation}
c^{s+1}\equiv{(c^\frac{s+1}{2})}^2\equiv{(c^\frac{\frac{p-1}{2}+1}{2})}^2\equiv{(c^\frac{p+1}{4})}^2\equiv c\ (mod\ p)
\end{equation}
$$
因此,同余式的解为
$$
\begin{equation}
m \equiv \pm c^{\frac{p+1}{4}}(mod\ p)
\end{equation}
$$
Rabin加密体制拓展分析
Rabin算法安全性能与效率分析
(1)效率高
RSA,ElGamal,的主要操作是模幂运算。该操作具有相当大的时间复杂度,这导致在实现非对称加密算法时效率降低。在Rabin密码系统中使用模块平方运算来生成加密文本,与其他非对称密码算法相比,这大大加快了加密过程,而不影响密码系统的安全性。Rabin
选择的加密指数 e = 2 很小, 因此, 加密速度相对较快, 可应用于软件产品。
(2)安全性强
1)求 x2 ≡ y (mod n) 等价于求n 的因子分解的困难性,根据目前大数分解的进展情况, 分解 n =2375的因数,大致要在亿次机上不间断的运行六十多年。
2)Rabin 解密过程基于求平方根的问题,Rabin密码系统对黑客攻击的抵抗,还涉及到模幂运算和解中国剩余定理,这两种程序都具有次指数时间复杂度,因此, 解密是比较困难的。
(3)与RSA相比较
RSA和Rabin的密码系统非常相似。两者都是基于因子分解的难度。主要区别在于,Rabin的密码系统等价于求整数因子分解一样困难,而解决RSA问题的方法还没达到因子分解的难度,这使得Rabin密码系统更加这样比RSA更安全。另一个区别是攻击的风险。Rabin密码系统对选择明文攻击是安全的,但是系统可能会被密码文本攻击破坏使攻击者能够知道私钥。RSA也是易受选定密文攻击,但私钥永远都是未知的。
(4)对于被动攻击是安全的
作为被动攻击者的任务是从密文消息c恢复出明文消息m。这就是平方根SQROOT问题。分解n和计算模n的平方根问题在计算上是等价的。因此,假定分解n在计算上不可能,Rabin公钥加密方案就可以证明能够抵抗被动攻击者的攻击。
破解攻击
有关Rabin的可能攻击
1)利用整数的因子分解
防范:选择p和q使得分解n是不可行的。
2)利用Rabin的乘性质
防范:冗余函数R是非乘性的。
对于选择密文攻击是不安全的
对于主动攻击者,Rabin公钥加密存在选择密文攻击问题。这样的攻击可以按如下步骤进行。攻击者选择一个随机整数m并计算c ≡ m2 (mod n)。攻击者提交 c 给 A 的解密机,它将解密c并返回某个明文消息y。由于A不知道明文消息m,并且m为随机选择,明文消息y未必就是同一个消息m。如果随机返回,将有1/2可能性,y不等于±m (mod n),在这种情况下,(m-y,n)就是n的一个素数因子。否则,攻击者可以换新的m重复以上过程。
针对选择密文攻击改进
冗余规则:Rabin公钥加密方案的一个缺点是接收者需要从4种可能情况中选择一个正确的解密明文消息。这一解密中的不确定问题在实践中可以通过预先增加定义原始明文消息冗余来解决。(例如,明文消息的最后64比特需要被复制。)这样,将有非常高的概率解密出来的4个可能明文消息中仅有一个符合冗余的规则。如果4个平方根中没有一个符合冗余规则,则接收者就认为出错而拒绝密文消息。
如果将冗余规则用于以上情况,则Rabin公钥加密方案将不再存在选择密文攻击问题。如果攻击者选择一条消息m并具有规定的冗余并将c≡ m2(mod n)提交给A的加密机,加密机将以非常高的概率返回消息m本身给攻击者(由于其它3个c的模平方根有非常大的概率不包含规定的冗余),则将不会提供给攻击者任何信息。另一方面,如果攻击者选择不包含冗余的消息m,则有非常高的可能性4个模平方根都不具有需要的冗余形式。在这种情况下,解密机将认为对c的解密失败并对攻击者不做答复。因此,Rabin公钥加密通过对增加适当的冗余规则将提高其实用价值。
Rabin加密体制代码编写与优化
Rabin-p算法
Rabin-p公钥密码体制
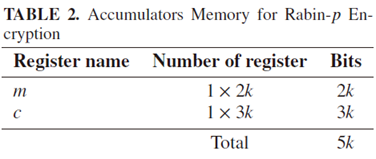
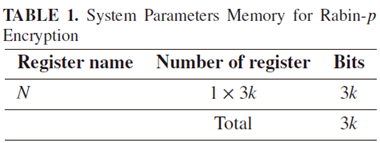
Rabin-p运行资源消耗
Encryption
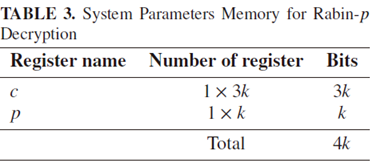
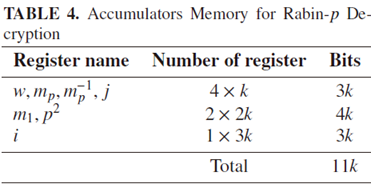
Decryption
Rabin-p运行时间消耗
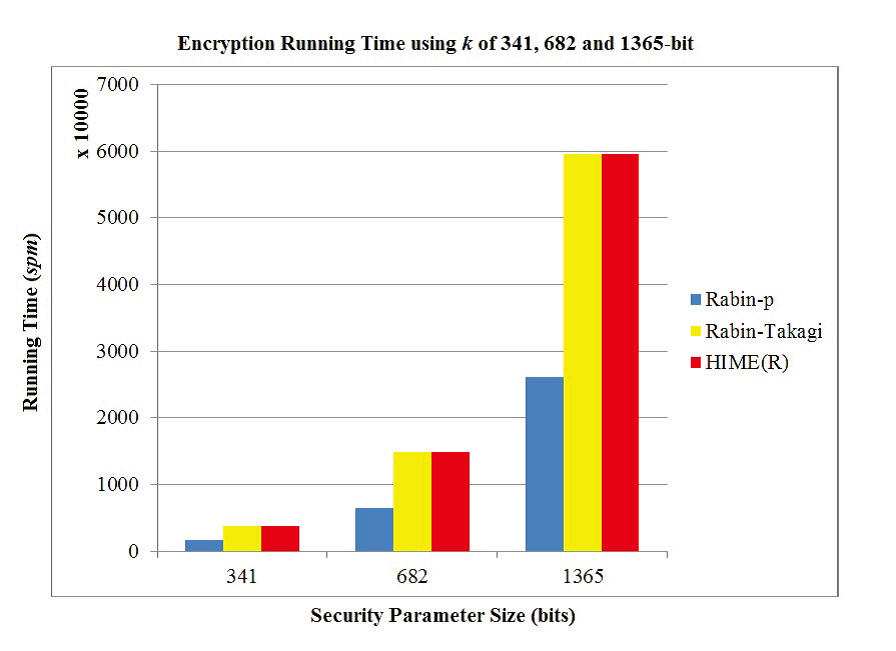
与其它算法时间的对比
FIGURE 1. Encryption Running Time using k of 341, 682 and 1365-bit
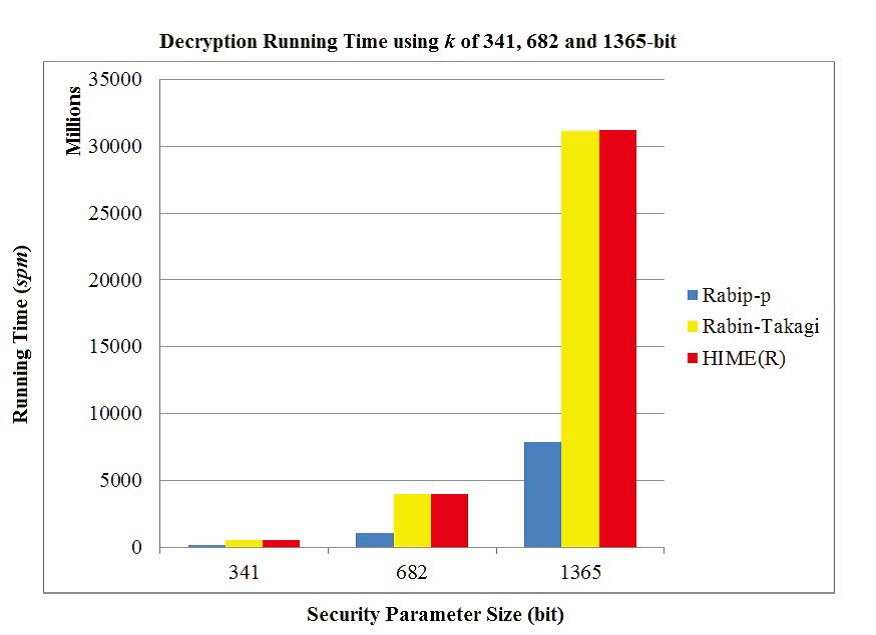
FIGURE 2. Decryption Running Time using k of 341, 682 and 1365-bit
运行时间
代码部分
Rabin加密体制
1 | # encoding: utf-8 |
Rabin加密体制-改进
1 | # encoding: utf-8 |
Rabin公钥加密体制的应用场景
Rabin公钥加密体制实际上就是一种RSA算法的特例,在实际应用中,Rabin公钥加密体制主要被用于签名算法。
数字签名算法
Rabin 密码系统可用于创建和验证数字签名。创建签名需要私钥 (p,q) , 验证签名需要公钥n.
签名:
一个消息 m<n 可以用私钥签名(p,q) 如下。
1.生成随机值 u.
2.使用加密哈希函数H 计算c=H(m|u),其中条形表示串联。c应该小于n.
3.对待 c作为 Rabin 加密的值并尝试使用私钥 (p,q) 对其进行解密.
这将产生通常的四个结果,r1, r2, r3, r4.
4.人们可能期望加密每个ri会产生c, 然而,这仅在以下情况下成立c恰好是二次残差p 和q. 要确定是否是这种情况,应加密第一个解密结果r1. 如果它没有加密到c, 用一个新的随机数重复这个算法. 在找到合适的算法之前需要重复此算法的预期次数c是4次.
5.找到了一个r1加密到c,签名是(r1,u).
验证签名:
一个签名(r,u)的m可以使用公钥进行验证n 如下。
1. 计算c=H(m|u)。
2. 使用公钥n加密r。
3. 当且仅当 r 等于c时签名有效。
下面展示一下Rabin数字签名算法的详细过程。
质数 $p$ 和 $q$,且有$ p \equiv 3 \pmod{4}$,$q \equiv 3 \pmod{4}$。组合 $(p, q)$ 为私钥,两数的乘积 $n = pq$ 为对应的公钥。使用私钥 $(p, q)$ 对消息 $m$ 签名的结果为组合 $(S, U)$,满足
$$
S^2 \equiv H(m||U) \pmod{n} \tag{1}
$$
其中的 $U$ 被称为填充值,$H(m||U)$ 的意思是将 $m$ 和 $U$ 的二进制流拼接在一起后再计算哈希,并将哈希结果(二进制流)看成一个整数。
令 $H = H(m||U) \bmod{n}$ 来简化书写。当 $U$ 确定后,可以用下式计算 S 的值。
$$
S = \left[q \cdot (H^{\frac{p+1}{4}} \bmod{p}) \cdot (q^{p-2} \bmod{p}) + p \cdot (H^{\frac{q+1}{4}} \bmod{q}) \cdot (p^{q-2} \bmod{q})\right] \bmod{n} \tag{2}
$$
这样便得到了一组 $(S, U)$,将结果代入 (1) 式验算,若成立则返回这组结果,反之则改变 $U$ 的值重新计算 $S$,直到找到一组满足 (1) 式的解。
请注意,当 $p \equiv 3 \pmod{4}$ 时,$\frac{p+1}{4}$ 是一个整数,同理 $\frac{q+1}{4}$ 也是一个整数。
签名时,通过循环在 $m$ 后追加字节 0x00 来改变 $H$ 的值,并在计算出 $S$ 后验证 (1) 式是否成立,是则跳出循环返回,否则继续寻找。
通过上面的描述你能看到,Rabin 签名的计算过程相对复杂,但验证过程极其简单。这个特性使得它非常适合在链上直接验签,虽然我们也可以在比特币脚本中实现 ECDSA 的验签逻辑,但它的计算成本要比验证 Rabin 签名高出许多。
整个算法设计基于这样的数学难题:在模是大合数的情况下,求二次剩余平方根是困难的。使用 Rabin 签名时,为了获得足够的安全性,公钥 $n$ 和哈希 $H(m||U)$ 的结果至少需要 3072 bits。
代码:
1 | def sign(p: int, q: int, digest: bytes) -> tuple: |
参考文献
- [1] W. Diffie and M. Hellman, IEEE Transactions On Information Theory 22, 644–654 (1976).
- [2] R. L. Rivest, A. Shamir, and L. Adleman, Communications Of The ACM 21,120–126 (1978).
- [3] M. O. Rabin, MIT Technical Report MIT/LCS/TR-212 (1979).
- [4] N. Koblitz and A. J. Menezes, Journal of Cryptology 20, 3–37 (2007).
- [5] D. Boneh, “Simplified OAEP For The RSA And Rabin Functions,” in Advances In Cryptology-Crypto 2001 (Springer, 2001), pp. 275–291.
- [6] S. D. Galbraith, Mathematics Of Public Key Cryptography (Cambridge University Press, 2012).
- [7] M. A. Asbullah and M. R. K. Ariffin, Malaysian Journal of Mathematical Sciences 11 (2016).
- [8] aaron67, Rabin 数字签名 (2021). https://aaron67.cc/2021/07/10/rabin-signatures/.